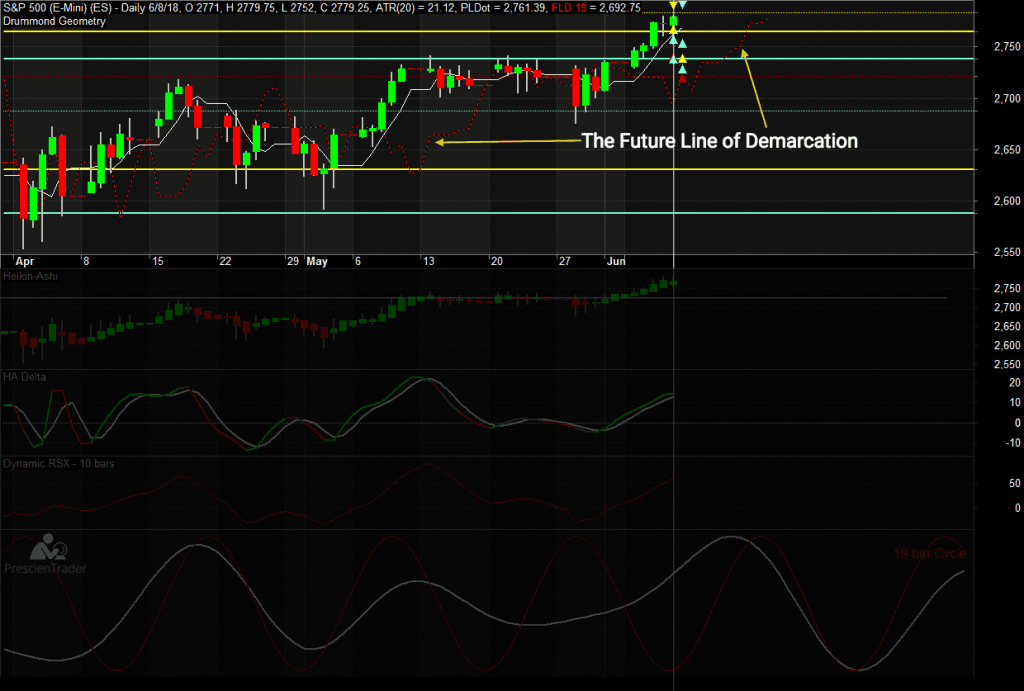
Der berühmte Fahrradforscher JM Hurst erfand die Zukünftige Demarkationslinie (FLD). Um den FLD zu zeichnen, musst du einfach Verschieben Sie das Preisdiagramm um eine halbe Zykluslänge nach vorne. Dies ist täuschend einfach und unglaublich mächtig. Wenn die Zykluslänge genau ist, Wenn der Kurs die FLD überschreitet, bestätigt er den letzten Höchst- oder Tiefststand für die entsprechende Zyklusfrequenz.
Die Analyse herkömmlicher Zyklen hängt in hohem Maße von den Wechselwirkungen zwischen Preis und FLD und dem prognostizierten Preis ab. Hurst entwickelte eine ausgefeilte Methodik, die beschreibt, wie verschiedene FLD-Muster und Preiswechselwirkungen zu interpretieren sind. Während Hursts Forschung viel Wert hat, entwickelte er seine Theorien vor der Erfindung moderner Computer. Daher umfasste die Durchführung einer konventionellen Zyklenanalyse nach Hursts Methodik viele Schritte und manuelle Berechnungen. In jüngerer Zeit wurden Softwareanwendungen entwickelt, die einen Großteil des Prozesses automatisieren und rationalisieren. Diese Anwendungen vereinfachen zwar die Durchführung einer Zyklusanalyse, sind jedoch immer noch durch ein vor mehr als 40 Jahren entwickeltes theoretisches Framework beschränkt. Anstatt die Wissenschaft voranzutreiben, automatisieren diese Anwendungen einfach alte Analysetechniken.
Als wir PrescienTrader entwickelten, begannen wir mit einem sauberen Schiefer. Wir haben Hursts Beiträge zur Wissenschaft der Zyklenanalyse anerkannt, wollten uns aber nicht auf eine über 40-jährige Methodik beschränken. Stattdessen haben wir Hursts Theorien objektiv getestet und sie in unsere Algorithmen aufgenommen, wenn sie Bestand hatten. Wir haben auch mit moderneren Algorithmen experimentiert, wie sie von Lars von Thienen von WhenToTrade.com. Wir fanden heraus, dass Lars 'Algorithmen Hursts in Bezug auf die Extraktion einzelner Zyklen aus dem Marktrauschen überlegen waren. Lars ging jedoch nicht auf das aus unserer Sicht wichtige Problem der Peak / Trough-Bestätigung ein, weshalb wir uns Hursts FLD-Theorien genauer anschauten. Letztendlich haben wir unsere Algorithmen so weiterentwickelt, dass sie alle Informationen enthielten, die sich aus der Analyse von FLD / Preis-Interaktionen gewinnen ließen, sodass eine komplexe FLD-Analyse für die Zwecke der Preisprognose überflüssig wurde. Wir waren dennoch der Meinung, dass eine schnelle FLD als Eintrittsauslöser verwendet werden kann, um unsere falschen Signale herauszufiltern. Unsere Tests haben dies bestätigt.
In unseren Diagrammen Die zukünftige Demarkationslinie wird im oberen Bereich als gestrichelte rote Linie angezeigt, die den Preis widerspiegelt, jedoch um eine halbe Zykluslänge nach vorne verschoben ist. Das angezeigte FLD passt sich dynamisch an die schnellste aktive Taktfrequenz an. Wenn die Prescient Line die Richtung ändert, warten wir, bis der Kurs die FLD überquert, bevor wir ein Einfahrtsignal ausgeben. Die Verwendung der schnellsten Zyklusfrequenz als Eintrittsauslöser ermöglicht es uns, den größten Teil der Bewegung zu erfassen und dennoch viele falsche Signale herauszufiltern.
Eine andere Verwendung für die zukünftige Demarkationslinie ist die Schätzung des Preisziels durch Beobachtung der Preisänderung zwischen dem Beginn eines Zyklus und dem Punkt, an dem es die FLD überschreitet. Da die FLD lediglich um eine halbe Zykluslänge vorwärtsgeschoben wird, kann davon ausgegangen werden, dass sie die Hälfte ihrer Gesamtstrecke für die Hälfte des Zyklus zurücklegt, wenn die Preise die FLD überschreiten. Wenn der Preis beispielsweise 100 ist, wenn ein Zyklus beginnt und er die FLD mit einem Preis von 105 überschreitet, können Sie ein Preisziel von 110 für den halben Zyklus schätzen. Das funktioniert aber oft ganz gut Die Auswirkungen von Unterstützungs- und Widerstandszonen werden nicht berücksichtigt. Wenn es im obigen Beispiel einen großen Widerstandsbereich bei 105 gibt, kann der Preis dort hängen bleiben, obwohl dies technisch nur zur Hälfte des Halbzyklus erfolgt. Somit, Bei der Festlegung von Preiszielen sollten Sie auch andere Ansätze berücksichtigen, z. B. Drummond Geometry.